History of Carnot cycle
Table of Contents
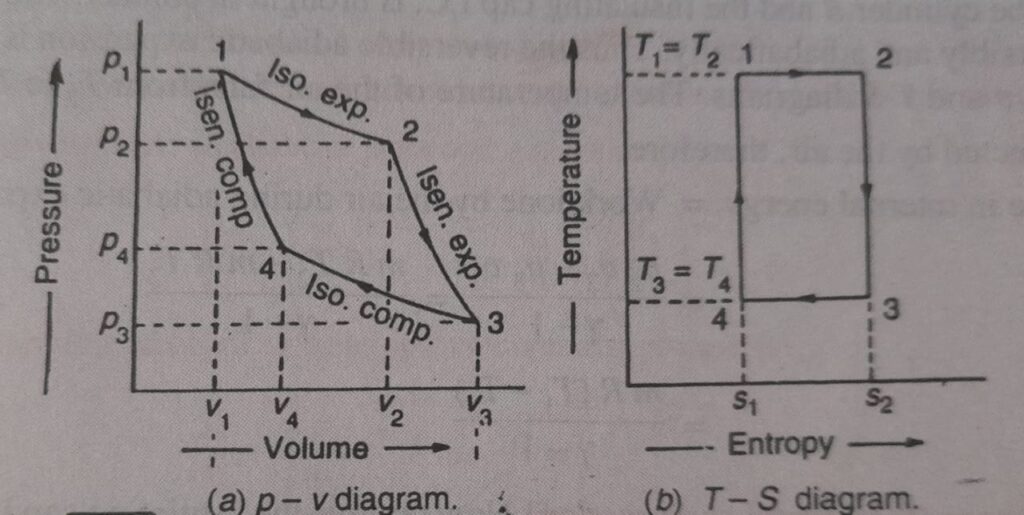
carnot cycle was devised by the scientist named “carnot” who was the first scientist to analyse the problem of the efficiency of heat engine disregarding its mechanical details. He focused his attention on the basic features of a heat engine. In a carnot cycle the working substance is subjected to a cyclic operation consisting of two isothermal and two reversible adiabatic process (also known as isentropic process). The PV and TS diagram of the cycle as shown in the figure below :
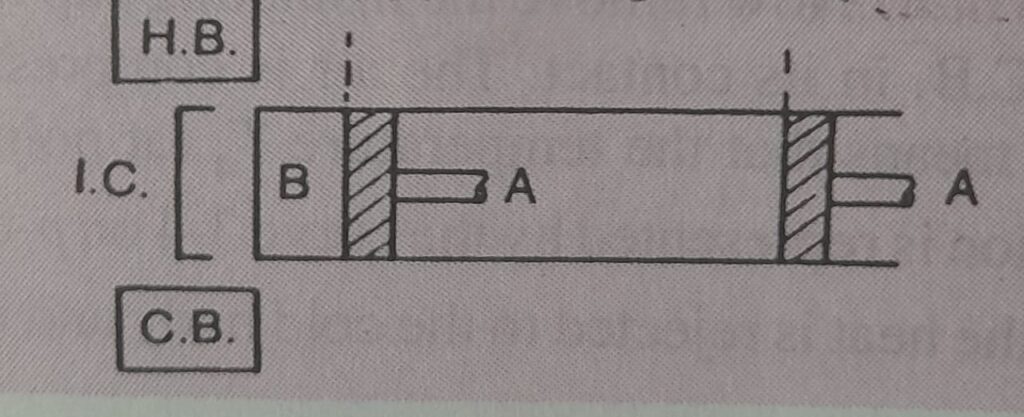
Initially the engine that was imagined by carnot has the air (which is supposed to behave like a perfect gas) as its working substance. Having enclosed in a cylinder in which a frictionless piston ‘A’ moves. The walls of the cylinder and piston are perfect non conductor of heat. however the bottom ‘B’ of the cylinder can be covered at will, by an insulating cap. The engine is assumed to work between two sources of infinite heat capacity, one at the higher temperature and other at the lower temperature.
Processes in Carnot cycle
Now, let us consider the four stages of the carnot cycle. Let the engine cylinder contain m kg of air at its original condition represented by point 1 on the PV and TS diagram. At this point, let P1, T1 and V1 be the pressure, temperature and volume of the air, respectively.
1.Isothermal expansion ( 1st stage)
The source i.e. hot body at a higher temperature is brought in contact with the bottom B of the cylinder. The air expands, practically at constant temperature it means that the temperature T2 at point 2 is equal to the temperature T1. This isothermal expansion is represented by curve 1-2 on PV and TS diagram. It may be noted that the heat supplied by the hot body is fully absorbed by the air and is utilised in doing external work.
i.e. Heat supplied = Work done by the air during isothermal expansion
Q1-2 = P1V1 loge (V2/V1)
= mRT1 loge (V2/V1)
= 2.3 mRT1 log r
Where, r = Expansion ratio = V2/V1
2.Reversible adiabatic or isentropic expansion (2nd stage)
The hot body is removed from the bottom of the cylinder B and the insulating cap is brought in contact. The air is allowed to expand reversibly and adiabatically. Thus the reversible adiabatic expansion is represented by the curve 2-3 on PV and TS diagrams. The temperature of the air falls from T2 to T3.
Since no heat is absorbed or rejected by the air, therefore
Decrease in internal energy = Work done by the air during adiabatic expansion.
= P2V2 – P3V3 / Y – 1
= mRT2 – mRT3 / Y – 1
3.Isothermal compression (3rd stage)
In this process the air is compressed practically at a constant temperature T3 from V3 to V4. It means that the temperature T4 is equal to the temperature T3. This isothermal compression is represented by the curve 3-4 on PV and TS diagrams. It would be seen that during this process the heat is rejected to the cold body and is equal to the work done on the air.
Heat rejected = Work done on the air during isothermal compression
= Q3-4 = P3V3 loge (V3/V4)
= mRT3 loge (V3/V4)
4.Reversible adiabatic aur isentropic compression (4th stage)
Now again the insulated cap is brought in contact with the bottom of the cylinder B and the air is allowed to be compressed reversibly and adiabatically. The reversible adiabatic compression is represented by the curve 4-1 on PV and TS diagrams. The temperature of the air increases from T4 to T1.
Since no heat is absorbed or rejected by the air, therefore
Increase in internal energy = Work done on the air during adiabatic compression
= P1V1 – P4V4 / Y-1
= mRT1 – mRT4 / Y-1
“Thus, we can see from above discussion that, the decrease in internal energy during reversible adiabatic expansion 2-3 is equal to the increase in internal energy during reversible adiabatic compression 4-1. Hence the net effect during the whole cycle is Zero.”
Efficiency of carnot cycle :
η = 1 – T3/T1
= 1 – (1/r)^Y-1
= 1 – 1/ r^Y-1
From the above equation, we see that the efficiency of Carnot’s cycle increases as T1 is increased or T3 is decreased. In other words, the heat should be taken in at as high a temperature as possible, and rejected as low a temperature as possible. It may be noted that 100% efficiency can be achieved, only if T3 reaches at absolute zero, though it is impossible to achieve in practice.
- In the above theory, we have taken temperature at points 1, 2, 3 and 4 as T1, T2, T3, and T4 respectively in order to keep similarity between Carnot cycle and other cycles. But at most of the places it is like T1 (for points 1 and 2) and T2 (for points 3 and 4). In that case, the obtained relation for efficiency as :
η = T1 – T2 / T1
= 1 – T2 / T1
- It may be noted that it is impossible to make an engine working on Carnot’s cycle The simple reason for the same is that the isothermal expansion 1-2 will have to be carried out extremely slow to ensure that the is always at temperature T1. Similarly, the isothermal compression 3-4 will have to be carried out extremely slow. But reversible adiabatic expansion 2-3 and reversible adiabatic compression 4-1 should be carried out an quick as possible, in order to approach ideal adiabatic conditions. We know that sudden changes in the speed of engine are not possible in actual practice. Moreover, it is impossible to completely eliminate friction between the various moving parts of the engine, and also heat losses due to conduction, radiation, etc. It is thus obvious that it is impossible to achieve Carnot’s engine in actual practice. However, such an imaginary engine is used as the ultimate standard of comparison of all heat engines.
That was all about the Carnot cycle, their processes, efficiency etc. Hope you all like this content. If this was helpful to you then kindly do share it with your friends. Also do follow us on social media platforms to bed aware of every mechanical engineering things happening all around.